Square Wheel Animations

Ein rollendes Qudrat — damit fing alles an!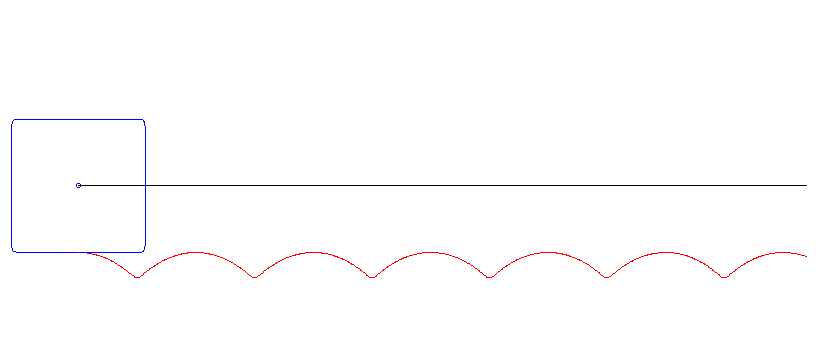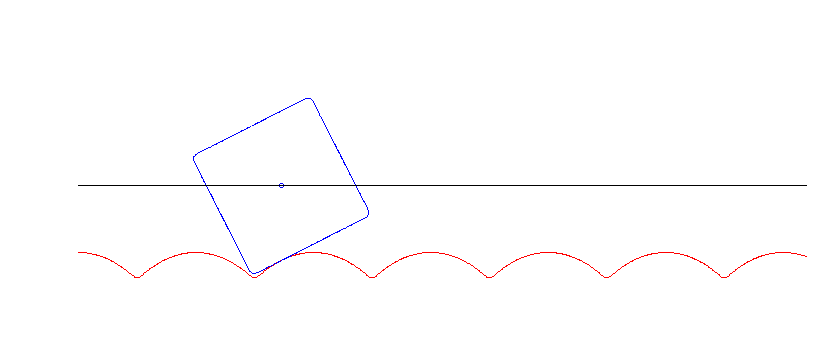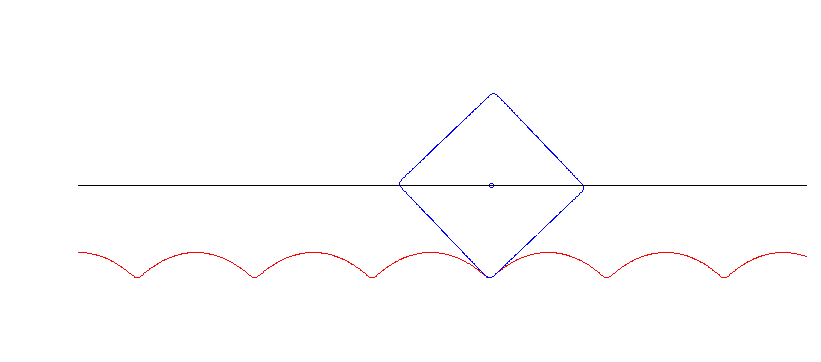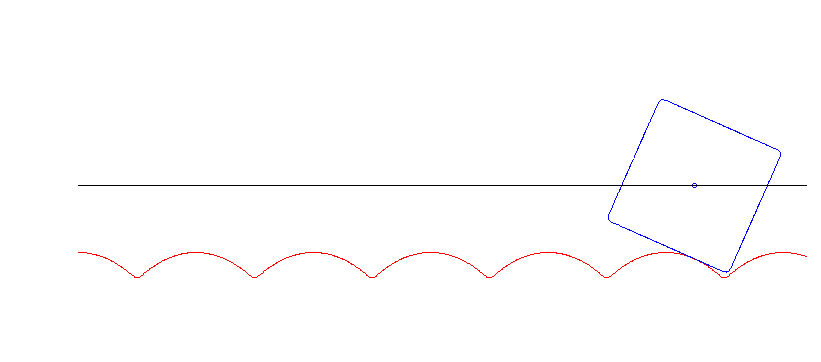

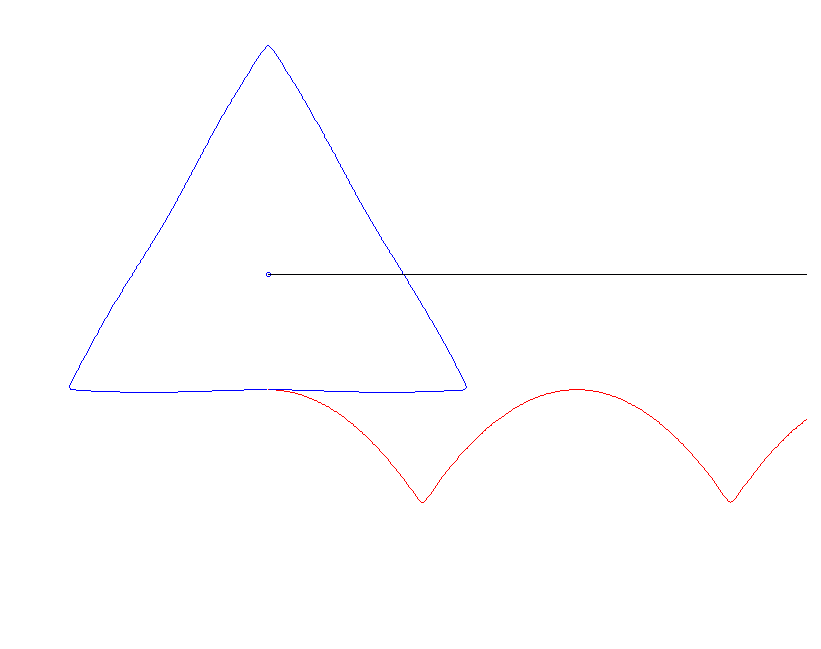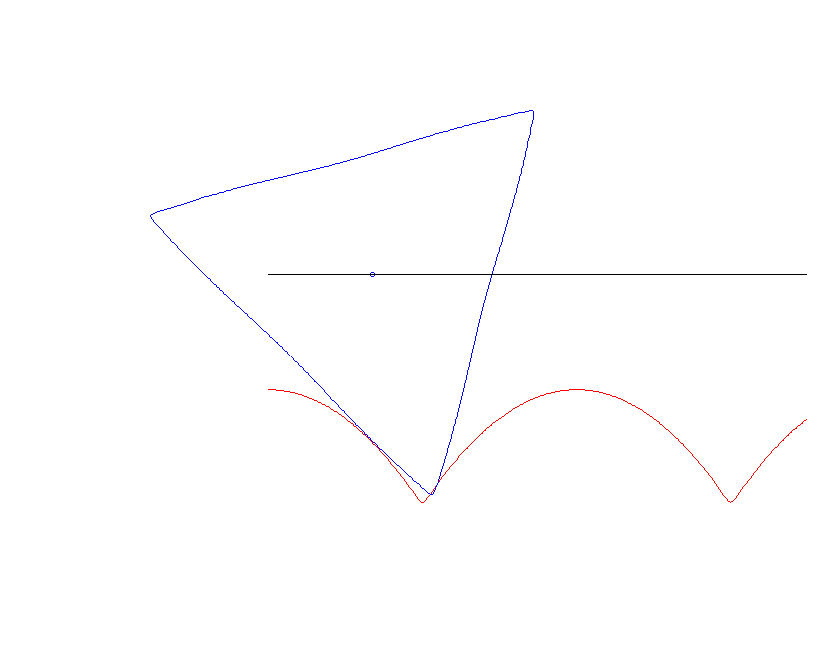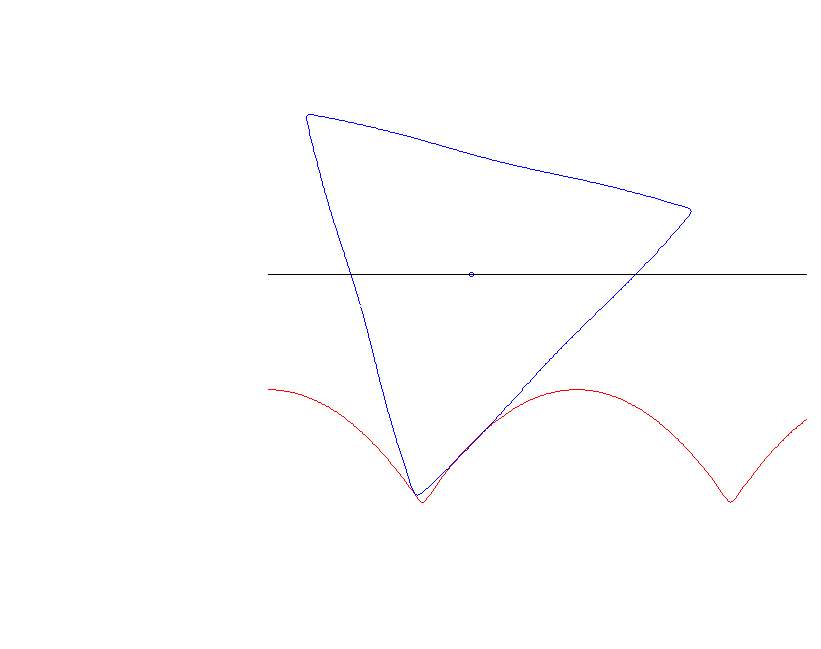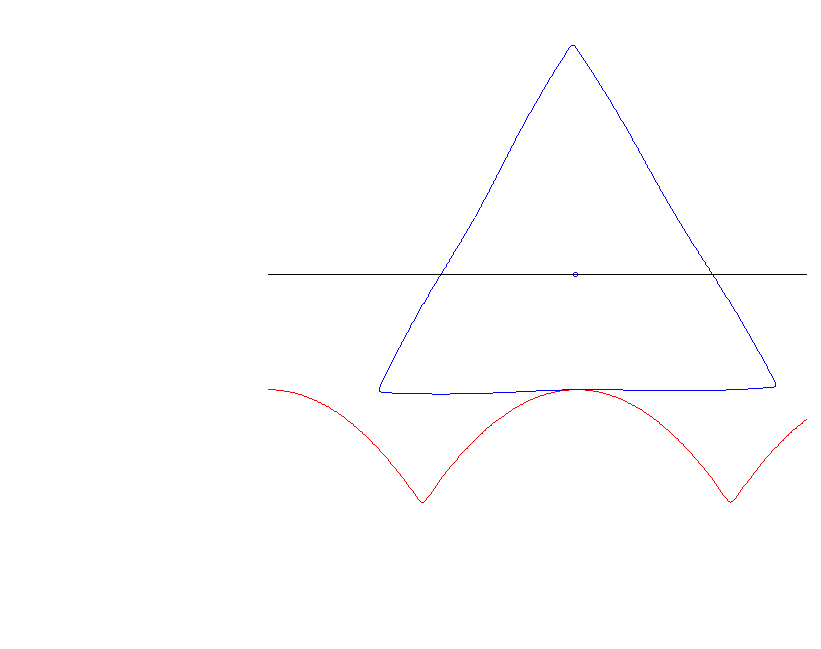
Ein Dreieck kann nicht rollen — es verhakt sich, allerdings kaum sichtbar, in der Unterlage.

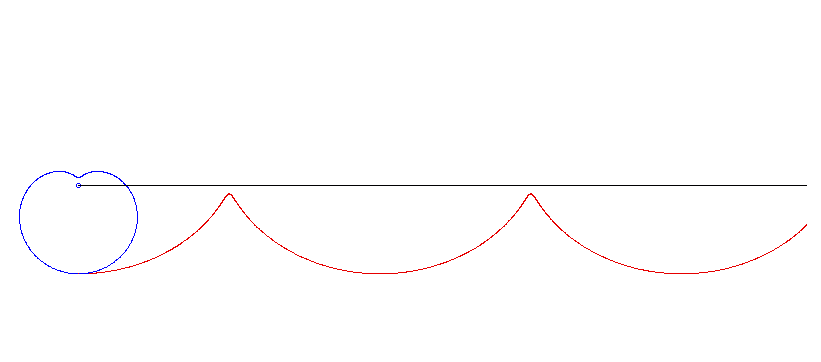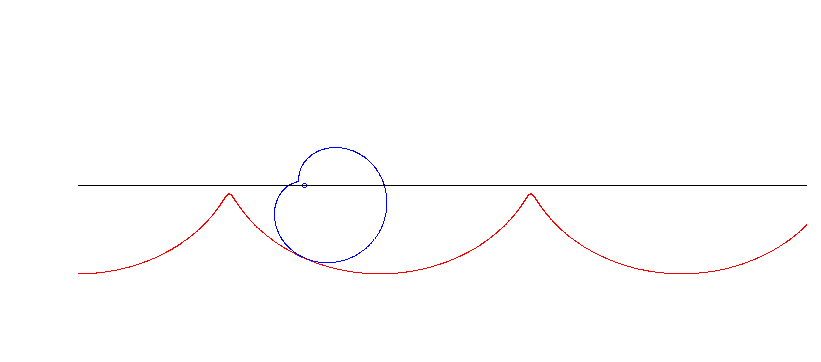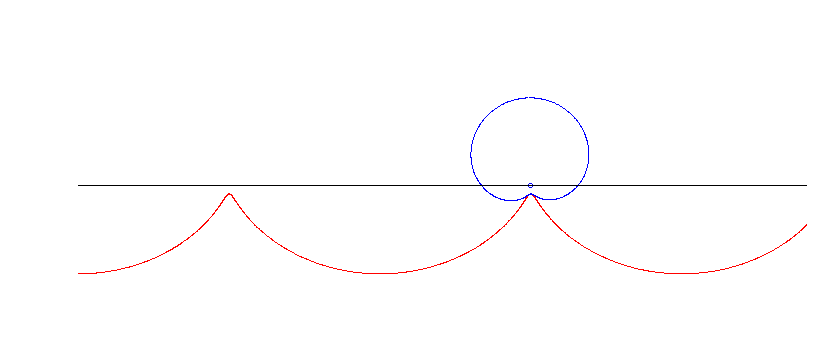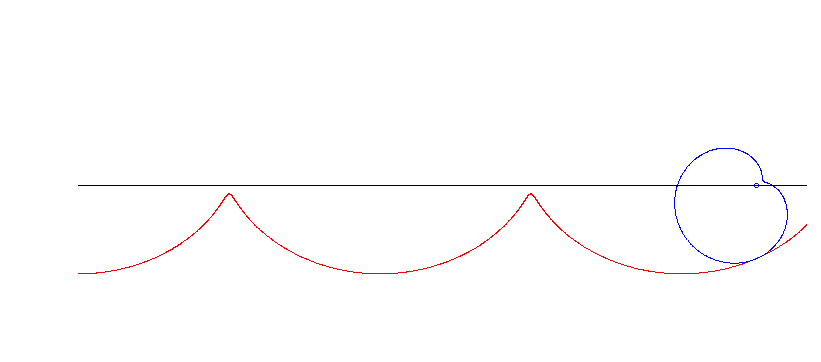
Eine Pascal'sche Schnecke (numerisch gerechnet, nicht im Skript).

Eine Parabel rollt auf einer kongruenten Parabel! (Nicht jede Parabel tut das, und sie tun es auch nicht in jedem Abstand, aber es gibt auch gleichzeitig nicht nur eine, die es tatsächlich tut, sondern eine ganze Schar)

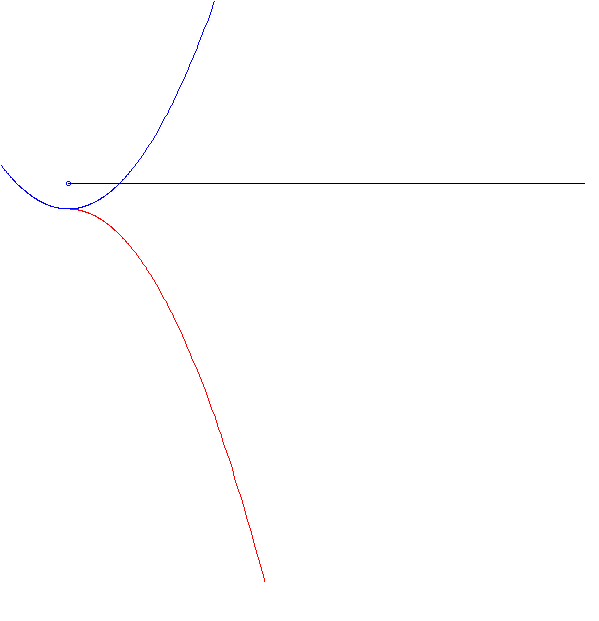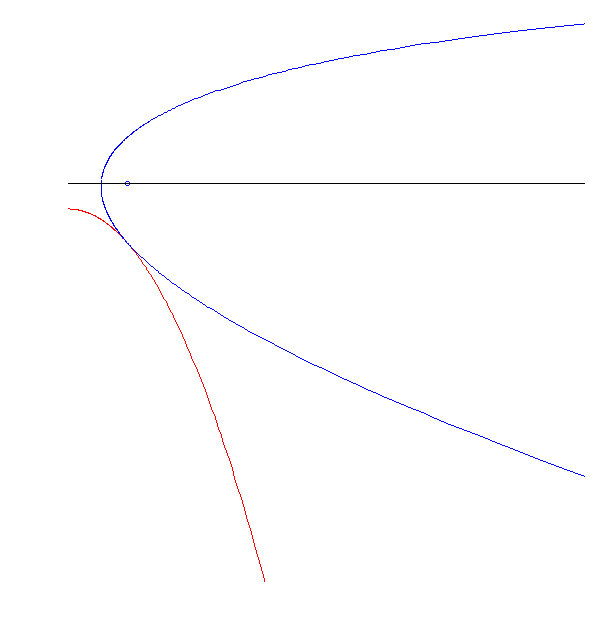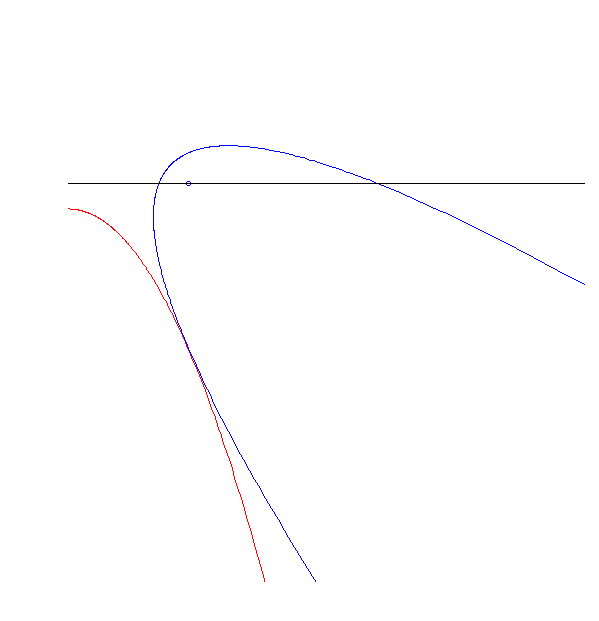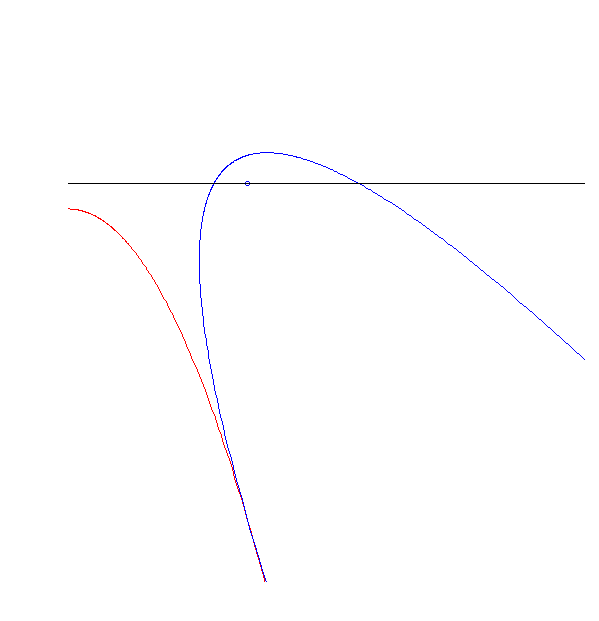
Die Achse dieser Ellipse geht durch einen ihrer Brennpunkte. In diesem Fall ist die Unterlage eine trigonometrische Funktion (verschobener, skalierter Sinus).

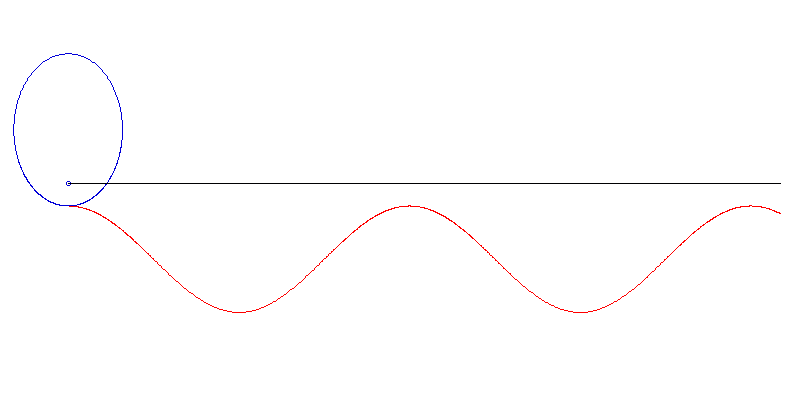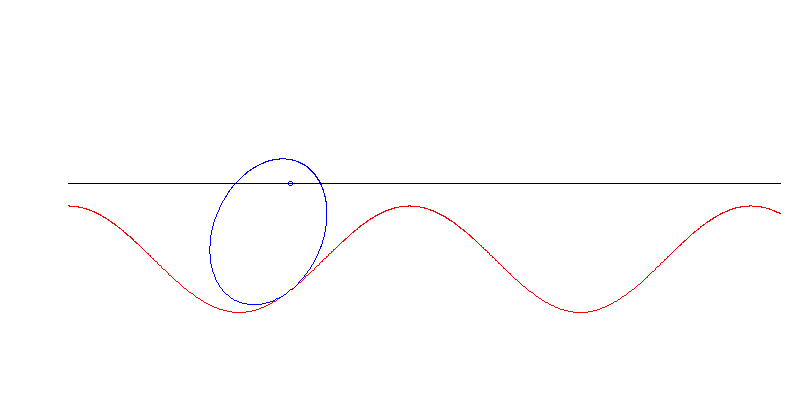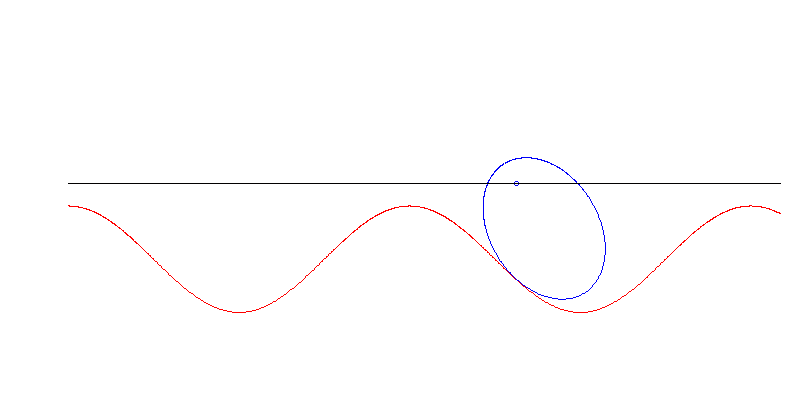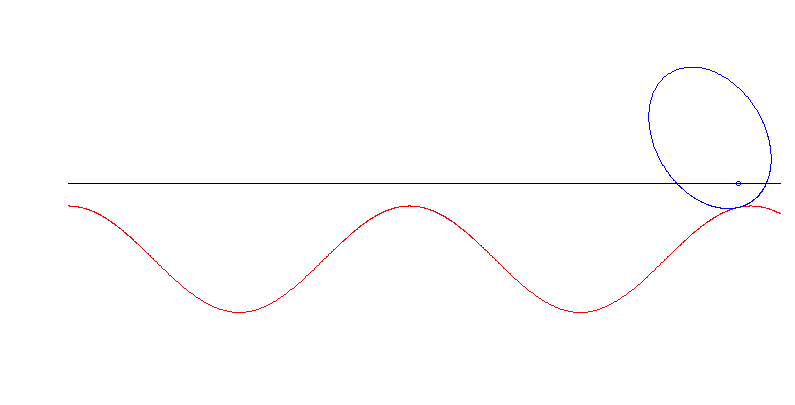
Ist die Ellipse hingegen im Zentrum fixiert, so führt das Problem, die Unterlage zu bestimmen, auf ein elliptisches Integral, das nicht mehr nett analytisch behandelt werden kann (auch wenn man einiges über dessen Inverse weiß).

Das Paar Zahnrad-Zahnstange wurde hier numerisch mithilfe der Superformel simuliert.

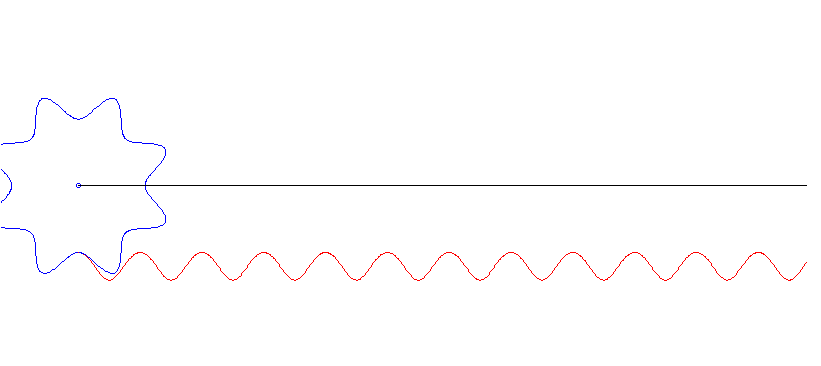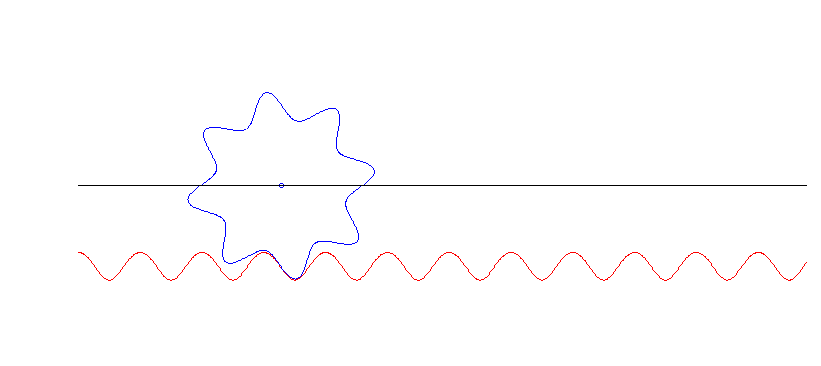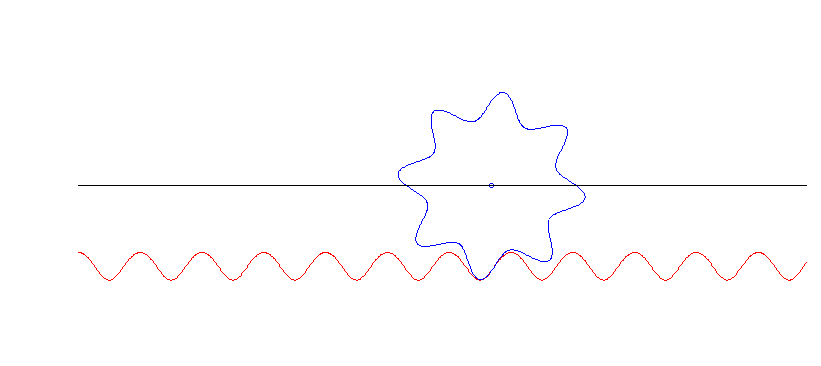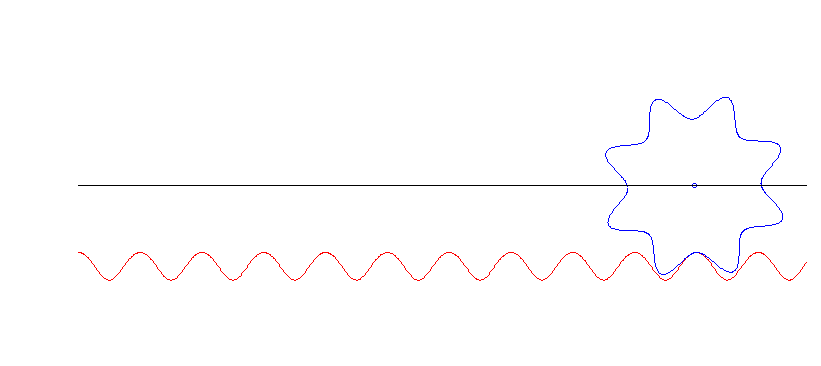
Diese Zahnräder sehen schon ziemlich echt aus, auch wenn das meines Wissens keine Zahnräder sind, die tatsächlich benutzt werden. (Die Zähne des linken Zahnrads sind von der Form const + sin(α) + 0.13 sin(3α), ein alter Trick aus der Fourier-Kiste).

Manchmal hat man hier den Eindruck, dass sich die Zahnräder verformen, anstatt zu drehen. Links wurde eine Ellipse mit (zugegeben — nur mäßig gut gelungenen Zähnen) angesetzt.

Hier sind zwei verallgemeinerte Ellipsen unterwegs, der Fall, der im Skript explizit durchgerechnet wird und wo der Achsabstand analytisch als Funktion des Zahnverhältnisses bekannt ist.

Last modified: Mon Jul 12 18:33:06 CEST 2021